RSA #20
The virtual quantum computer (VQC) is a grid made of constructably infinite elements that follow a known pattern. It is indexed using e, n, and t, where e is the column, n is the row, and t is the specific element in the cell.
The grid in its entirety serves as the superposition. The required input parameters to collapse the superposition are d and e, which are trivial to calculate for all c that is the difference of two squares. When the integers that are the difference of two squares are arranged into the grid and their corresponding properties are shown, a pattern emerges that shows a path to calculate the factors of c instead of searching for them. It can be understood using only the basic operations of arithmetic and sqrt. All currently-known patterns can be found within one thread here >>6506
C# VQC generator - pastebin.com/XFtcAcrz
Java VQC generator - pastebin.com/2MPYrJVe
Python VQC generator - pastebin.com/NZkjtnZL
Glossary
Look-up
A pattern used to calculate the factors of c, like a value look-up table.
Column
All cells for a given e
Row
All cells for a given n
Cell
All entries for a given e,n (not to be confused with an entry itself.)
Entry; record; element
A set of variables corresponding to a factorization for a given c. The legend to read entries is {e:n:d:x:a:b} (e, n, t) = c
Example: {1:5:12:7:5:29} (1, 5, 4) = 145
ab record; nontrivial factorization
The element that contains the factorization of c that is not 1*c, hence, nontrivial.
1c record; trivial factorization
The element generated from setting a=1 and b=c
Mirror element
The element in -f corresponding to an element in e, in the context of a given c.
Variables
a and b are, to reiterate, the factors of c. a is the smaller factor of c, and b is the larger one.
d is the integer square root of c.
e is the remainder of taking the integer square root of c. Unless c is a perfect square, a remainder will be left over.
i is the root of the large square. It is equal to (d+n).
j is the root of the small square. it is equal to (x+n).
n is what you add to d to be exactly halfway between a and b, and it is the root of the large square, so it takes you from d to the large square.
x is what you add to a to make d. When added to n it makes the root of the small square.
f is what you add to c to make a square. (e is what you subtract from c to make the square below it, f adds to make the square above c.)
t is the third coordinate in the VQC, it is a function of x.
q is a product created by multiplying successive primes until the product is above d.
u is the triangle base of (x+n)^2. 8 times the triangle number of u plus one is (x+n)^2 for c with odd x+n.
ab = c
dd + e = c
(d + n)(d + n)-(x + n)(x + n) = c
a + 2x + 2n = b
a = d - x
d = a + x
d = floor_sqrt(c)
e = c - (dd)
b = c / a
n = ((a + b) / 2) - d
d + n = i
x = d - a
x = (floor_sqrt(( (d+n)*(d+n) - c))) - n
x + n = j
j^2 = 8*T(u) + 1
f = e - 2d + 1
u = (x+n) / 2
if (e is even) t = (x + 2) / 2
if (e is odd) t = (x + 1) / 2
Past threads
RSA #0 - archive.fo/XmD7P
RSA #1 - archive.fo/RgVko
RSA #2 - archive.fo/fyzAu
RSA #3 - archive.fo/uEgOb
RSA #4 - archive.fo/eihrQ
RSA #5 - archive.fo/Lr9fP
RSA #6 - archive.fo/ykKYN
RSA #7 - archive.fo/v3aKD
RSA #8 - archive.fo/geYFp
RSA #9 - archive.fo/jog81
RSA #10 - archive.fo/xYpoQ
RSA #11 - archive.fo/ccZXU
RSA #12 - archive.fo/VqFge
RSA #13 - archive.fo/Fblcs
RSA #14 - archive.fo/HfxnM
RSA #15 - archive.vn/59GwR
RSA #16 - archive.vn/F49fw
RSA #17 - archive.vn/u2Tu6
RSA #18 - archive.is/FDVP9
RSA #19 - archive.is/6mJhe

Grid Patterns
VQC:
At this point, a good strategy would be to have a thread that is used to post patterns from The End grid.
Patterns that apply to all c in the grid.
Patterns that apply to all cells in a row.
Patterns that apply to all cells in a column.
Special rows.
Special columns.
It was hinted before and was useful to me, by enumerating all the patterns in one place, the answer will materialise.
You are looking for a key shortcut.
The grid does the ALL the work for you.
Suggestion…
Either here or a worker thread(s), discuss each rule or pattern.
When consensus is reached, put the rule or pattern in the key thread.
This process and result of this process may surprise you, more than you think.
It may change the way you think.
It may be advantage you can apply in other problem solving.
This is how you win.

Welcome to /vqc/. New people tend to have some trouble understanding what this board is about, so this thread serves as an explanation. The long and detailed version will follow in the replies to this post. Here’s a shortened version:
>early on during the beginning of Q in November of last year
>someone calling themselves VQC starts posting Q-style crumbs to the annoyance of most and the curiosity of others
>makes some interesting claims, such as Agartha being real
>starts posting code around the end of November, calling it a Virtual Quantum Computer (hence the name) with unlimited qubits
>says it can be used to prove that P=NP, to factorize semiprimes (which allows us to break RSA encryption), and overall to demonstrate new mathematic principles that have been hidden from the public by the elite
>suggests that making these mathematic principles public is an important part of the idea of the public having freedom, despite it meaning large changes to encryption being necessary
>the code uses two numbers, i and j, to calculate several variables
>i and j are implemented in a nested loop, which in simple terms means j starts at 0 and increases by 1 each time the variables are calculated until it is equal to i, at which point i, which also started at 0, increases by 1, and j starts at 0 again
>a = i-j, b = i+j, and the other variables are calculated from these
>in the context of factorizing semiprimes, the two variables a and b multiply together and give us c, and if a and b are prime numbers, c is a semiprime
>semiprimes are a key component of RSA encryption because of the fact that, with current factorization methods, it would take thousands of years to factorize 1024-bit semiprimes, making it seemingly unreasonable to crack
>the variables are put into a spreadsheet (which we call The End) with the variable e as the x axis and the variable n as the y axis
>several anons have been working together for the last 7 months to try to figure out how we can use the grid to factorize semiprimes
>VQC continues to post crumbs occasionally and guide us in the right direction
>if VQC told us explicitly how it all worked, it would defeat the purpose
>we are all very far down the track from the beginning in November now, so there is a lot of information that (a) new people will need to read through before they can get up to speed with the rest of us, and (b) that those of us who have been here the whole time or most of the time won’t always remember, and thus being forgetful might be keeping us from solving it
>according to VQC, we’re very, very close to figuring it out
>also according to VQC, there are infinite other possibilities in regards to what we can do with this grid once we’re ready
A more detailed explanation that would make this a one-stop place for anyone new is currently in progress. If there’s anything specific you would like to know, ask about it in the RSA general sticky. I’m keeping this thread locked so it can be specifically for the explanation and the congregation of all of our findings so far, so any suggestions can go in the meta thread, which is >>193 here.

Meta thread
Board rules:
>no spam - this includes posting over and over that you think VQC is LARPing with no evidence, or trying to derail any of the general threads with irrelevant information
That's pretty much it. You're only going to get banned if you seem to be intentionally shitting up the place, and if that's the case we'll try asking you to stop first.
This thread is dedicated to the way the board is run. If you have any suggestions about how we should do things, or you think any other posters are causing trouble, feel free to discuss it here.
AA/ArchiveAnon is the board owner, and he can be privately contacted at thebuttonnexttocapslocktwice@protonmail.com. We would all prefer if you would ask about things on the board so that everything is public, though. If you think I'm doing a bad job of running the board, don't hesitate to mention why so I can stop doing whatever I'm doing. If you think I've become a tyrannical dictator and that I'm not listening to your criticisms, the nature of this website is such that you can start a new VQC-related board, and our community is small enough that you wouldn't have any trouble convincing everyone to join you if they agreed. This board is not about me; it's about the collaborative effort.
There is also a /vqc/ Discord server. Ask Topol either in RSA general or his EZ Bake general thread if you'd like to join. This Discord server is strictly for off-topic conversations and half-baked ideas that we don't think are worth posting here on the board. We are all dedicated to making this a public disclosure, so if you think some of us are plotting behind closed doors, you're welcome to join the server and post screenshots to the board.
The End

Topol's EZ Bake Oven
A-Notations:
1. I speak in onions.
2. I have no idea what you need right now.
3. I'm just trying to figure out existence.
4. Feel free to put random notes and ideas here.
5. You don't know what I'm looking for, either.
6. Think of this as a thread to pluck while working on music.
7. There are no stupid questions, only faggots.
8. Imagine VQC as a Shamanic Journey Guide.
9. 369, 9 To 3, 12, 1+2=3, it works all the way up.

Sonoluminescence
As requested by VQC:
"Is there anyone more practical with access to 3D printing as we can run the sonoluminescence thread in parallel and it will be quite rewarding to build a fully functioning cold fusion generator?
Perfectly safe, boils water.
Thought it may be fun for those who prefer to build stuff."

RSA #19
The virtual quantum computer (VQC) is a grid made of constructably infinite elements that follow a known pattern. It is indexed using e, n, and t, where e is the column, n is the row, and t is the specific element in the cell.
The grid in its entirety serves as the superposition. The required input parameters to collapse the superposition are d and e, which are trivial to calculate for all c that is the difference of two squares. When the integers that are the difference of two squares are arranged into the grid and their corresponding properties are shown, a pattern emerges that shows a path to calculate the factors of c instead of searching for them. It can be understood using only the basic operations of arithmetic and sqrt. All currently-known patterns can be found within one thread here >>6506
C# VQC generator - pastebin.com/XFtcAcrz
Java VQC generator - pastebin.com/2MPYrJVe
Python VQC generator - pastebin.com/NZkjtnZL
Glossary
Look-up
A pattern used to calculate the factors of c, like a value look-up table.
Column
All cells for a given e
Row
All cells for a given n
Cell
All entries for a given e,n (not to be confused with an entry itself.)
Entry; record; element
A set of variables corresponding to a factorization for a given c. The legend to read entries is {e:n:d:x:a:b} (e, n, t) = c
Example: {1:5:12:7:5:29} (1, 5, 4) = 145
ab record; nontrivial factorization
The element that contains the factorization of c that is not 1*c, hence, nontrivial.
1c record; trivial factorization
The element generated from setting a=1 and b=c
Mirror element
The element in -f corresponding to an element in e, in the context of a given c.
Variables
a and b are, to reiterate, the factors of c. a is the smaller factor of c, and b is the larger one.
d is the integer square root of c.
e is the remainder of taking the integer square root of c. Unless c is a perfect square, a remainder will be left over.
i is the root of the large square. It is equal to (d+n).
j is the root of the small square. it is equal to (x+n).
n is what you add to d to be exactly halfway between a and b, and it is the root of the large square, so it takes you from d to the large square.
x is what you add to a to make d. When added to n it makes the root of the small square.
f is what you add to c to make a square. (e is what you subtract from c to make the square below it, f adds to make the square above c.)
t is the third coordinate in the VQC, it is a function of x.
q is a product created by multiplying successive primes until the product is above d.
u is the triangle base of (x+n)^2. 8 times the triangle number of u plus one is (x+n)^2 for c with odd x+n.
ab = c
dd + e = c
(d + n)(d + n)-(x + n)(x + n) = c
a + 2x + 2n = b
a = d - x
d = a + x
d = floor_sqrt(c)
e = c - (dd)
b = c / a
n = ((a + b) / 2) - d
d + n = i
x = d - a
x = (floor_sqrt(( (d+n)*(d+n) - c))) - n
x + n = j
j^2 = 8*T(u) + 1
f = e - 2d + 1
u = (x+n) / 2
if (e is even) t = (x + 2) / 2
if (e is odd) t = (x + 1) / 2
Past threads
RSA #0 - archive.fo/XmD7P
RSA #1 - archive.fo/RgVko
RSA #2 - archive.fo/fyzAu
RSA #3 - archive.fo/uEgOb
RSA #4 - archive.fo/eihrQ
RSA #5 - archive.fo/Lr9fP
RSA #6 - archive.fo/ykKYN
RSA #7 - archive.fo/v3aKD
RSA #8 - archive.fo/geYFp
RSA #9 - archive.fo/jog81
RSA #10 - archive.fo/xYpoQ
RSA #11 - archive.fo/ccZXU
RSA #12 - archive.fo/VqFge
RSA #13 - archive.fo/Fblcs
RSA #14 - archive.fo/HfxnM
RSA #15 - archive.vn/59GwR
RSA #16 - archive.vn/F49fw
RSA #17 - archive.vn/u2Tu6
RSA #18 - archive.is/FDVP9

VA's Programming For Newfags
==Want to learn how to program?== =#MeToo.=
Alright, let's talk about it faggots. I don't know shit about programming, but I love to learn. Luckily, we have excellent program anons who can help. Just ran my first snippet of code today, "Hello World". All anons welcome, this is a forum for asking questions and getting answers. Also, ProgramAnons can pose skill appropriate challenges for us newbs if they think we're ready or if they just want to mess with us. Goal is to help everyanon advance in their coding or teaching skillz.
-VA
RSA #18
The virtual quantum computer (VQC) is a grid made of constructably infinite elements that follow a known pattern. It is indexed using e, n, and t, where e is the column, n is the row, and t is the specific element in the cell.
The grid in its entirety serves as the superposition. The required input parameters to collapse the superposition are d and e, which are trivial to calculate for all c that is the difference of two squares. When the integers that are the difference of two squares are arranged into the grid and their corresponding properties are shown, a pattern emerges that shows a path to calculate the factors of c instead of searching for them. It can be understood using only the basic operations of arithmetic and sqrt. All currently-known patterns can be found within one thread here >>6506
C# VQC generator - pastebin.com/XFtcAcrz
Java VQC generator - pastebin.com/2MPYrJVe
Python VQC generator - pastebin.com/NZkjtnZL
Glossary
Look-up
A pattern used to calculate the factors of c, like a value look-up table.
Column
All cells for a given e
Row
All cells for a given n
Cell
All entries for a given e,n (not to be confused with an entry itself.)
Entry; record; element
A set of variables corresponding to a factorization for a given c. The legend to read entries is {e:n:d:x:a:b} (e, n, t) = c
Example: {1:5:12:7:5:29} (1, 5, 4) = 145
ab record; nontrivial factorization
The element that contains the factorization of c that is not 1*c, hence, nontrivial.
1c record; trivial factorization
The element generated from setting a=1 and b=c
Mirror element
The element in -f corresponding to an element in e, in the context of a given c.
Variables
a and b are, to reiterate, the factors of c. a is the smaller factor of c, and b is the larger one.
d is the integer square root of c.
e is the remainder of taking the integer square root of c. Unless c is a perfect square, a remainder will be left over.
i is the root of the large square. It is equal to (d+n).
j is the root of the small square. it is equal to (x+n).
n is what you add to d to be exactly halfway between a and b, and it is the root of the large square, so it takes you from d to the large square.
x is what you add to a to make d. When added to n it makes the root of the small square.
f is what you add to c to make a square. (e is what you subtract from c to make the square below it, f adds to make the square above c.)
t is the third coordinate in the VQC, it is a function of x.
q is a product created by multiplying successive primes until the product is above d.
u is the triangle base of (x+n)^2. 8 times the triangle number of u plus one is (x+n)^2 for c with odd x+n.
ab = c
dd + e = c
(d + n)(d + n)-(x + n)(x + n) = c
a + 2x + 2n = b
a = d - x
d = a + x
d = floor_sqrt(c)
e = c - (dd)
b = c / a
n = ((a + b) / 2) - d
d + n = i
x = d - a
x = (floor_sqrt(( (d+n)*(d+n) - c))) - n
x + n = j
j^2 = 8*T(u) + 1
f = e - 2d + 1
u = (x+n) / 2
if (e is even) t = (x + 2) / 2
if (e is odd) t = (x + 1) / 2
Past threads
RSA #0 - archive.fo/XmD7P
RSA #1 - archive.fo/RgVko
RSA #2 - archive.fo/fyzAu
RSA #3 - archive.fo/uEgOb
RSA #4 - archive.fo/eihrQ
RSA #5 - archive.fo/Lr9fP
RSA #6 - archive.fo/ykKYN
RSA #7 - archive.fo/v3aKD
RSA #8 - archive.fo/geYFp
RSA #9 - archive.fo/jog81
RSA #10 - archive.fo/xYpoQ
RSA #11 - archive.fo/ccZXU
RSA #12 - archive.fo/VqFge
RSA #13 - archive.fo/Fblcs
RSA #14 - archive.fo/HfxnM
RSA #15 - archive.vn/59GwR
RSA #16 - archive.vn/F49fw
RSA #17 - archive.vn/u2Tu6
RSA #17
The virtual quantum computer (VQC) is a grid made of constructably infinite elements that follow a known pattern. It is indexed using e, n, and t, where e is the column, n is the row, and t is the specific element in the cell.
The grid in its entirety serves as the superposition. The required input parameters to collapse the superposition are d and e, which are trivial to calculate for all c that is the difference of two squares. When the integers that are the difference of two squares are arranged into the grid and their corresponding properties are shown, a pattern emerges that shows a path to calculate the factors of c instead of searching for them. This pattern can be understood using only the basic operations of arithmetic and sqrt.
Glossary
Look-up
A pattern used to calculate the factors of c, like a value look-up table.
Column
All cells for a given e
Row
All cells for a given n
Cell
All entries for a given e,n (not to be confused with an entry itself.)
Entry; record; element
A set of variables corresponding to a factorization for a given c. The legend to read entries is {e:n:d:x:a:b} (e, n, t) = c
Example: {1:5:12:7:5:29} (1, 5, 4) = 145
ab record; nontrivial factorization
The element that contains the factorization of c that is not 1*c, hence, nontrivial.
1c record; trivial factorization
The element generated from setting a=1 and b=c
Mirror element
The element in -f corresponding to an element in e, in the context of a given c.
Sieve
A sieve is an algorithm for factoring integers arising out of number theory in the 1900s, most notably from Carl Pomerance.
Smoothness
A number is described as smooth if it is composed of small prime factors, opposed to large ones.
Sqrt Tree
The sqrt tree is a structure created by recursively taking d and e starting with c, creating a tree with several to many branches. (Changed from remainder to sqrt because there is more than one tree).
Triangle Tree
The triangle tree is a similar structure but uses the T-1 function instead of sqrt.
Functions
na transform
A movement from a record in (e, n) into (e,1) where n becomes 1 and a becomes a times the n of the (e,n) record. It has also been used to refer to moving n*a records down in a cell.
Pell(n)
The nth Pell number function. Can be calculated recursively or formulaically using the square root of 2.
ST(n)
The nth square triangular number. A square triangular number is a number that is both a square and a triangle number. The Pell function is used to calculate square triangular numbers.
T(n)
The triangle number function.
Example: T(7) = the 7th triangle number
T-1(n), inverse T
The inverse triangle number function.
Example: T(7th triangle number) = 7
Variables
a and b are, to reiterate, the factors of c. a is the smaller factor of c, and b is the larger one.
d is the integer square root of c.
e is the remainder of taking the integer square root of c. Unless c is a perfect square, a remainder will be left over.
i is the root of the large square. It is equal to (d+n).
j is the root of the small square. it is equal to (x+n).
n is what you add to d to be exactly halfway between a and b, and it is the root of the large square, so it takes you from d to the large square.
x is what you add to a to make d. When added to n it makes the root of the small square.
f is what you add to c to make a square. (e is what you subtract from c to make the square below it, f adds to make the square above c.)
t is the third coordinate in the VQC, it is a function of x.
q is a product created by multiplying successive primes until the product is above d.
u is the triangle base of (x+n)^2. 8 times the triangle number of u plus one is (x+n)^2 for c with odd x+n.
h was a variable used to quantify families of numbers. The way to calculate it is currently unknown.
When capitalized versions of the variables are used in comparison to lowercase versions, the capitalized versions refer to the variable's value for the trivial record, and the lowercase variables refer to the values for the nontrivial record. Sometimes these trivial uppercase variables are referred to with "Big" preceding the letter.
{e:N:d:X:A:B} (e, N, T) is the trivial element.
{e:n:d:x:a:b} (e, n, t) in this context is the nontrivial element, the prime factorization of c.
Since under this rule D and E would refer to the same variable as d and e and thus be redundant, D and E have been defined as references to elements.
D and D2 refer to the two elements whose d[t] values d from c is between in row one.
Since N and n are references to specific values, R is used to refer to an element pair whose a[t] values are the estimates of n provided by D and D2.
E refers to any element whose values are a starting estimate of the factorization of c (ie i0, j0, n0, x0, etc).
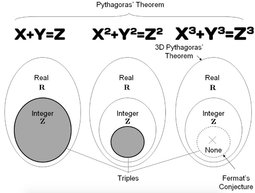
Fermat's Last Theorem general #1
>The other thread will describe how to take the work done to solve Fermat Last theorem relates to our approach and why two objects that are identical types in number theory had to be proved so in a difficult to under proof, when in reality, with the right number system or model, this should have been obvious or a tautology.
Fermat's Last Theorem: there are no three positive integers a, b and c that satisfy the equation a^n + b^n = c^n for any n>=3.
You can read about the work done to solve Fermat's Last Theorem here:https://en.wikipedia.org/wiki/Wiles%27s_proof_of_Fermat%27s_Last_Theorem
It involves the modularity theorem and elliptic curves, both of which VQC has already mentioned.
>The next piece that uses the same approach is not going to go into the details of elliptic curves and modular forms, it will be more about why these two identical things looked different, because realising they were the same thing solved a 350 year old math problem called Fermat's Last Theorem.
>What does it tell us about a language like maths when you need a virtually incomprehensible proof JUST to show two things are identical?

RSA #16 - "Larp Inception" edition
Virtual Quantum Computer
The virtual quantum computer (VQC) is a grid made of constructably infinite elements that follow a known pattern.
The grid in its entirety serves as the superposition. The input parameters that collapse the superposition are d and e, which are trivial to calculate for all c that is the difference of two squares. When the integers that are the difference of two squares are arranged into the grid and their corresponding properties are shown, a pattern emerges that shows a path to calculatethe factors of c instead of searching for them.
The grid is indexed using e, n, and t, where e is the column, n is the row, and t is the specific element in the cell.
Glossary
Look-up
A pattern used to calculate the factors of c, like a value look-up table.
Column
All cells for a given e
Row
All cells for a given n
Entry; record; element
A set of variables corresponding to a factorization for a given c. The legend to read entries is {e:n:d:x:a:b} (e, n, t) = c
Example: {1:5:12:7:5:29} (1, 5, 4) = 145
ab record; nontrivial factorization; prime element
The element that contains the factorization of c that is not 1*c, hence, nontrivial.
1c record; trivial factorization
The element generated from setting a=1 and b=c
Mirror element
The element in -f corresponding to an element in e, in the context of a given c.
Cell
All entries for a given e,n (not to be confused with an entry itself.)
Sieve
A sieve is an algorithm for factoring integers arising out of number theory in the 1900s, most notably from Carl Pomerance.
Smoothness
A number is described as smooth if it is composed of small prime factors, opposed to large ones.
Remainder Tree
The remainder tree is a structure created by recursively taking d and e starting with c, creating a tree with several to many branches.
Functions
na transform
A movement from a record in (e, n) into (e,1) where n becomes 1 and a becomes a times the n of the (e,n) record. It has also been used to refer to moving n*a records down in a cell.
Pell(n)
The nth Pell number function. Can be calculated recursively or formulaically using the square root of 2.
ST(n)
The nth square triangular number. A square triangular number is a number that is both a square and a triangle number. The Pell function is used to calculate square triangular numbers.
T(n)
The triangle number function.
Example: T(7) = the 7th triangle number
T-1(n), inverse T
The inverse triangle number function.
Example: T(7th triangle number) = 7
Variables
a and b are, to reiterate, the factors of c. a is the smaller factor of c, and b is the larger one.
d is the integer square root of c.
e is the remainder of taking the integer square root of c. Unless c is a perfect square, a remainder will be left over.
i is the root of the large square. It is equal to (d+n).
j is the root of the small square. it is equal to (x+n).
n is what you add to d to be exactly halfway between a and b, and it is the root of the large square, so it takes you from d to the large square.
x is what you add to a to make d. When added to n it makes the root of the small square.
f is what you add to c to make a square. (e is what you subtract from c to make the square below it, f adds to make the square above c.)
t is the third coordinate in the VQC, it is a function of x.
q is a product created by multiplying successive primes until the product is above d.
u is the triangle base of (x+n)^2. 8 times the triangle number of u plus one is (x+n)^2 for c with odd x+n.
h was a variable used to quantify families of numbers. The way to calculate it is currently unknown.
When capitalized versions of the variables are used in comparison to lowercase versions, the capitalized versions refer to the variable's value for the trivial record, and the lowercase variables refer to the values for the nontrivial record. Sometimes these trivial uppercase variables are referred to with "Big" preceding the letter.
{e:N:d:X:A:B} (e, N, T) is the trivial element.
{e:n:d:x:a:b} (e, n, t) in this context is the nontrivial element, the prime factorization of c.

Solution Patterns Thread
Remember all those times you took the difference of some value or the remainder of some value from c and a solution value surfaced, but it didn't work for other example c values?
Well, inspired by those lists of values I developed that happen to make x and x+n show up somewhere, I don't think those paths are useless coincedences and should be forgotten, I think we should make a list of them.

RSA #15 - "All Your Base Are Belong To Us" Edition
The virtual quantum computer (VQC) is a grid made of infinite yet constructable sets that follow a known pattern. Like a quantum spreadsheet.
The grid is the superposition. The collapse of that superposition will be two input parameters, d and e which can be calculated easily for all integers, c, where c is the difference of two squares. Its purpose and our goal is to learn and show the TRUTH, one of them being P=NP. Cracking RSA will be a consequence.
When the integers that are the difference of two squares are arranged into the grid and their corresponding properties are shown, a pattern emerges that shows calculation instead of searching is possible.
Glossary
Column
All cells for a given e.
Row
All cells for a given n
The grid is indexed using e, n, and t, where e is the rows, n is the columns, and t is the specific element in the cell.
Entry, record, element
one set of variables that represents one factorization for a number.
an entry = {e:n:d:x:a:b} (e, n, t)
{1:5:12:7:5:29} (1, 5, 4) is a record AKA an element AKA an entry.
ab record, nontrivial factorization, prime record
the element that contains the factorization of c that is not 1*c, hence, nontrivial.
1c record, trivial factorization
the element generated from setting a=1 and b=c
Cell
All entries for a given e,n (not to be confused with an entry itself.)
Genesis cell
e,1
Remainder Tree
The remainder tree is the result of treating d and e as c's recursively until 1 is reached, creating a tree with several to many branches.
Functions
na transform
a movement from a record in (e, n) into (e,1) where n becomes 1 and a becomes a times the n of the (e,n) record. It has also been used to refer to moving n*a records down in a cell.
T
T of number or T(input) is the triangle number function. If our input is 7, T(7) returns the 7th triangle number
T-1, inverse T
the inverse function of the triangle number function that returns the index of a given triangle number. If our input is the 7th triangle number, the function returns 7.
Variables
The map's legend is {e:n:d:x:a:b}, where c is any number that is the difference of two squares, so odd numbers are included. It is the number you want to factor. It is the number that the a and b in an entry multiply to make.
a and b are, to reiterate, the factors of c. a is the smaller factor of c, and b is the larger one.
d is the integer square root of c
e is the remainder of taking the integer square root of c. Unless c is a perfect square, a remainder will be left over.
i is the root of the large square. it is the same thing as (d+n)
j is the root of the small square. it is the same thing as (x+n). i^2 - j^2, difference of squares.
n is what you add to d to be exactly halfway between a and b, and it is the root of the large square. So it takes you from d to the large square.
x is what you add to a to make d. When added to n it makes the root of the small square.
f is what you add to c to make a square. (e is what you subtract from c to make the square below it, f adds to make the square above c.)
g is the square root of c with decimals, opposed to d, which discards decimals.
t is the third coordinate in the VQC, it is a function of x.
u is the base of a triangle that helps us calculate (x+n) for certain c values. simply put, it is a representation of (x+n). 8 times the triangle number of u plus one is x+n.
s was a variable used to demonstrate patterns in (e, 1). See "(e, 1)."
When capitalized versions of the variables are used in comparison to lowercase versions, the capitalized versions refer to the variable's value for the trivial record, and the lowercase variables refer to the values for the nontrivial record.
{e:N:d:X:A:B} (e, N, T) is the trivial element.
{e:n:d:x:a:b} (e, n, t) in this context is the nontrivial element, the prime factorization of c.

Old Bread Rehash
This thread is for the purpose of examining old breads, for those of us starting late. This will allow us to work without detracting from the main RSA threads, and hopefully help us to catch up sooner rather than later.
Here are links to archives from /cbts, and older breads–you'll find relevant links in all of them:
RSA #0 —— https://archive.fo/XmD7P
RSA #1 —— https://archive.fo/RgVko
RSA #2 —— https://archive.fo/fyzAu
RSA #3 —— https://archive.fo/uEgOb
RSA #4 —— https://archive.fo/eihrQ
RSA #5 —— ,>>7
RSA #6 —— ,>>848
RSA #7 —— ,>>1713
RSA #8 —— ,>>2555
RSA #9 —— ,>>3361
RSA #10 —— ,>>4140
RSA #11 —— ,>>5042
RSA #12 —— ,>>5844
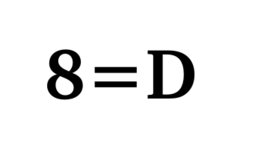
RSA #14
The virtual quantum computer (VQC) is a grid made of infinite yet constructable sets that follow a known pattern. Like a quantum spreadsheet.
The grid is the superposition. The collapse of that superposition will be two input parameters, d and e which can be calculated easily for all integers, c, where c is the difference of two squares. Its purpose and our goal is to learn and show the TRUTH, one of them being P=NP. Cracking RSA will be a consequence.
When the integers that are the difference of two squares are arranged into the grid and their corresponding properties are shown, a pattern emerges that shows calculation instead of searching is possible.
Glossary
Column
All cells for a given e.
Row
All cells for a given n
The grid is indexed using e, n, and t, where e is the rows, n is the columns, and t is the specific element in the cell.
Entry, record, element
one set of variables that represents one factorization for a number.
an entry = {e:n:d:x:a:b} (e, n, t)
{1:5:12:7:5:29} (1, 5, 4) is a record AKA an element AKA an entry.
ab record, nontrivial factorization, prime record
the element that contains the factorization of c that is not 1*c, hence, nontrivial.
1c record, trivial factorization
the element generated from setting a=1 and b=c
Cell
All entries for a given e,n (not to be confused with an entry itself.)
Genesis cell
e,1
Remainder Tree
The remainder tree is the result of treating d and e as c's recursively until 1 is reached, creating a tree with several to many branches.
Functions
na transform
a movement from a record in (e, n) into (e,1) where n becomes 1 and a becomes a times the n of the (e,n) record. It has also been used to refer to moving n*a records down in a cell.
T
T of number or T(input) is the triangle number function. If our input is 7, T(7) returns the 7th triangle number
T-1, inverse T
the inverse function of the triangle number function that returns the index of a given triangle number. If our input is the 7th triangle number, the function returns 7.
Variables
The map's legend is {e:n:d:x:a:b}, where c is any number that is the difference of two squares, so odd numbers are included. It is the number you want to factor. It is the number that the a and b in an entry multiply to make.
a and b are, to reiterate, the factors of c. a is the smaller factor of c, and b is the larger one.
d is the integer square root of c
e is the remainder of taking the integer square root of c. Unless c is a perfect square, a remainder will be left over.
i is the root of the large square. it is the same thing as (d+n)
j is the root of the small square. it is the same thing as (x+n). i^2 - j^2, difference of squares.
n is what you add to d to be exactly halfway between a and b, and it is the root of the large square. So it takes you from d to the large square.
x is what you add to a to make d. When added to n it makes the root of the small square.
f is what you add to c to make a square. (e is what you subtract from c to make the square below it, f adds to make the square above c.)
g is the square root of c with decimals, opposed to d, which discards decimals.
t is the third coordinate in the VQC, it is a function of x.
u is the base of a triangle that helps us calculate (x+n) for certain c values. simply put, it is a representation of (x+n). 8 times the triangle number of u plus one is x+n.
s was a variable used to demonstrate patterns in (e, 1). See "(e, 1)."
When capitalized versions of the variables are used in comparison to lowercase versions, the capitalized versions refer to the variable's value for the trivial record, and the lowercase variables refer to the values for the nontrivial record.
{e:N:d:X:A:B} (e, N, T) is the trivial element.
{e:n:d:x:a:b} (e, n, t) in this context is the nontrivial element, the prime factorization of c.

CA's D Navigation
Since this is exactly what we don't want to be doing, I created a seperate thread for it. Also I don't have the batter for the other one. I'll probably jump back into the new thread once it is created.
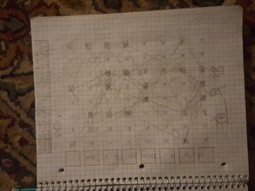
I have devised a way to generate the (e,n,d) coordinates for any d value. This requires new rules. For now, I'm ignoring the x,a,b,c values because they aren't required for this pattern. That said, if we analyze steps of this pattern we may have patterns in x,a,b,c, I just haven't checked yet. I'm still trying to validate if this is the case. Also, for this, you generate (e,n,d,x,a,b,c) values through END(e,n,d) which is posted in my other code dump
(E,N,D,O,T)
Pic related is for D = 6.
On this graph, the +'s indicate a value that was generated by theend(1500) code. The *'s indicate a suspected d at that value. Whether or not the *'s actually correspond to a cell we can overlook for now, because the pattern seems to hold.
O is the origin cell of a line. Indicated by the integers in the chart (except for the 6,7,8,9 on the line). 0 is the zero origin, 1 is the 1 origin etc.
For each origin cell, the value of T is 0. For the cell on the N+1 row relative to an origin line, we have T = T+1. The T's for O=1 are written for T=6,7,8,9
Now that you can read the values, here are the rules I've discovered:
(-D^2, -D, D, 0, 0) is a valid start record for any D
(e,n,d,o,t) -> (e+t^2, n, d, o+t, 0) (to generate origin cell for same row given any cell)
(e,n,d,o,t) -> (e+2o, n+1, d, o, t+1) (to get next t) *
(e,n,d,o,t) -> (e-2o, n-1, d, o, t-1) (to get prevoius t) *
(e,n,d,o,0) -> (e+2ot, n+t, d, o, t) (any t from origin) (basically the same as the two * above)
(e,n,d,o,0) -> (e-t^2, n, d, o-t, t) (to generate other cells in row n from t=0) (t<o)
(e,n,d,o,t) -> (e+ (2t-1), n, d, o+1, t-1) (to shift from o to o+1)
(e,n,d,o,t) -> (e- (2t+1), n, d, o-1, t+1) (shift from o to o-1)
*BIG* (e,n,d,o,t) -> (e+2d-1, n-1, d-1, o,t)
This last equation comes from noticing that the layout of all the D grids is the EXACT SAME, just with a different 0 origin cell.
To factor C, our record (e,n,d,x,1,c) has the correct D already. I suspect that we can generate the correct O and T values from some other method to zip right to our correct cell.

RSA Lucky #13
The virtual quantum computer (VQC) is a grid made of infinite yet constructable sets that follow a known pattern. Like a quantum spreadsheet.
The grid is the superposition. The collapse of that superposition will be two input parameters, d and e which can be calculated easily for all integers, c, where c is the difference of two squares. Its purpose and our goal is to learn and show the TRUTH, one of them being P=NP. Cracking RSA will be a consequence.
When the integers that are the difference of two squares are arranged into the grid and their corresponding properties are shown, a pattern emerges that shows calculation instead of searching is possible.
Glossary
Column
All cells for a given e.
Row
All cells for a given n
The grid is indexed using e, n, and t, where e is the rows, n is the columns, and t is the specific element in the cell.
Entry, record, element
one set of variables that represents one factorization for a number.
an entry = {e:n:d:x:a:b} (e, n, t)
{1:5:12:7:5:29} (1, 5, 4) is a record AKA an element AKA an entry.
ab record, nontrivial factorization, prime record
the element that contains the factorization of c that is not 1*c, hence, nontrivial.
1c record, trivial factorization
the element generated from setting a=1 and b=c
Cell
All entries for a given e,n (not to be confused with an entry itself.)
Genesis cell
e,1
Remainder Tree
The remainder tree is the result of treating d and e as c's recursively until 1 is reached, creating a tree with several to many branches.
Functions
na transform
a movement from a record in (e, n) into (e,1) where n becomes 1 and a becomes a times the n of the (e,n) record. It has also been used to refer to moving n*a records down in a cell.
T
T of number or T(input) is the triangle number function. If our input is 7, T(7) returns the 7th triangle number
T-1, inverse T
the inverse function of the triangle number function that returns the index of a given triangle number. If our input is the 7th triangle number, the function returns 7.
Variables
The map's legend is {e:n:d:x:a:b}, where c is any number that is the difference of two squares, so odd numbers are included. It is the number you want to factor. It is the number that the a and b in an entry multiply to make.
a and b are, to reiterate, the factors of c. a is the smaller factor of c, and b is the larger one.
d is the integer square root of c
e is the remainder of taking the integer square root of c. Unless c is a perfect square, a remainder will be left over.
i is the root of the large square. it is the same thing as (d+n)
j is the root of the small square. it is the same thing as (x+n). i^2 - j^2, difference of squares.
n is what you add to d to be exactly halfway between a and b, and it is the root of the large square. So it takes you from d to the large square.
x is what you add to a to make d. When added to n it makes the root of the small square.
f is what you add to c to make a square. (e is what you subtract from c to make the square below it, f adds to make the square above c.)
g is the square root of c with decimals, opposed to d, which discards decimals.
t is the third coordinate in the VQC, it is a function of x.
u is the base of a triangle that helps us calculate (x+n) for certain c values. simply put, it is a representation of (x+n). 8 times the triangle number of u plus one is x+n.
s was a variable used to demonstrate patterns in (e, 1). See "(e, 1)."
When capitalized versions of the variables are used in comparison to lowercase versions, the capitalized versions refer to the variable's value for the trivial record, and the lowercase variables refer to the values for the nontrivial record.
{e:N:d:X:A:B} (e, N, T) is the trivial element.
{e:n:d:x:a:b} (e, n, t) in this context is the nontrivial element, the prime factorization of c.

Intro to ECC
ECC starting from the basics.
If you can understand what mod means,
if you can understand graphing points,
if you can understand arithmetic,
if you can understand logarithms,
You can understand ECC. Maybe you'll even get to see how they're modular forms..
and what a modular form is.
I will walk through it from start to finish. I'll start by listing the prerequisites to ECC. There aren't many. A novice can understand.
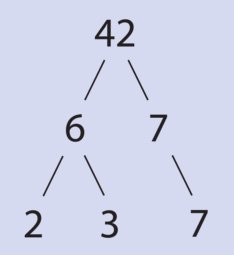
Logarithms
All a logarithm is, is calculating n in picture 2, where b and x are given. The following articles and the 2nd picture should clarify.
https://www.mathsisfun.com/algebra/logarithms.html
https://simple.wikipedia.org/wiki/Logarithm
The Discrete Logarithm Problem
So now that we have established what a logarithm is, then we can understand this easily. The Discrete Logarithm Problem (DLP) is the problem of calculating n in bⁿ = x, where we know b and x. Aside from certain cases (which do not apply to where you encounter them in cryptography), there is no known efficient method for computing this.
Diffie-Helmann
https://youtube.com/watch?v=YEBfamv-_do
https://youtube.com/watch?v=ESPT_36pUFc
https://youtube.com/watch?v=Yjrfm_oRO0w
These videos and picture 3 should clarify how the Diffie-Helmann cryptosystem uses the DLP to encrypt, decrypt and sign messages.
Galois Fields
Will be explained in the next posts.
EC Arithmetic
Will be explained in the next posts.
Spooky scary skeletons
Would anyone be interested in some explanation of what "occultism" means and how all of this spooky stuff people have been alluding to works? I know at least several if not most of you have expressed a belief in the idea that we as a group of people were meant to come together as we did (Chris included), but for most it seems to just be to the point of knowing that there's more to what's going on than we're aware (likely in part because of some of what Q has said). Of course, maybe some of you even know more than I do. That said, I've been studying, reading etc for the last three years, and I feel I know enough that I could shed light on some important things, such as reasons to believe consciousness isn't physical, how Kek works, how reality works in relation to this stuff, etc.
I'm well aware that, from an outsider's perspective, whenever most of you have read about this kind of thing, you probably thought it was stupid, meaningless word salad with no practical application. That was me before I delved into it (I was an agnostic atheist). I've always tried as hard as possible to understand the theory behind things, rather than being one of those people who says "namaste" all the time and regurgitates useless bullshit like "you need to raise your vibration and become one with the universe, man; open your third eye" without understanding anything. You can all easily find this information by scouring the internet (there are even a few boards here, such as >>>/fringe/, although the board culture there is discouraging), but if anyone would like, I could explain stuff like pic related (something Chris retweeted), answer questions, provide books (I have thousands) and point people in the right direction.

Hobo's Math Camp
So, like any good hobo I have been around. Also, I have done some camping. A few people talked about meeting up and camping would be a good way to do it. Its cheap. Its fun, Its public, and its different.
So my favorite place to camp is Western Oregon. I never miss a summer out that way and this year is no different. So I hereby propose a math camp for everyone here.
To really make it happen we will need a chunk of time that everyone can make it. My window is from May through Aug. I recommend Late May/early June as this is the best weather, and minimal chance of us getting smoked out… Well smoked out from forest fires.
I will be in the area with all my shit for camping so it will be easy for me to set it up more or less and I can do transportation from either Portland or Eugene Airports. Portland is kinda far though so I would like to make just one trip there if possible.
Coordination will the the hard part so lets start with dates., Post your dates below and lets see what lines up..

RSA #12
VQC sez: "(You) are at The final lock and key construction steps. Happy to give it but it is the Eureka moment and anons are close. In hindsight, it shows exactly why this problem has existed for so long.You are solving two problems at once in this method of constructing the answer. Also in hindsight the steps give the pattern back in the grid (The End).
RSA #13
The Grid is also called The End.
The Grid has cells.
Each cells has zero or infinite elements.
That a cell has infinite elements if it has any, is the first part to show.
An element represents a product, c.
c is the difference of two squares.
ab = c = dd + e = (d+n)(d+n) - (x+n)(x+n)
An element that represents a product c, the difference of two squares has a column coordinate and row coordinate.
The column coordinate is e, the remainder of taking the largest square with sides d.
The row coordinate is n, the amount added to d to make the side of the larger square in the difference of two squares. n is also the amount added to d to make it the mid point of a and b.
Each cell has coordinates (e,n)
Each cell element has coordinates (e,n,t) where t is where the element comes in the cell if ordered by size of c.
Each element c in a cell has the properties (e,n,d,x,a,b)
e is the remainder and column
n is the amount added to d to make the large square
d is the square root of c
x is the difference of a and d
a if the smaller factor of c if not equal to b
b is the larger factor of c if not equal to a

Bitcoin discussion and crash thread
Bitcoin Price Drops 22% in Four Days as Infighting Goes Public
Original — fortune.com/2017/12/21/bitcoin-price-drops-infighting/
Archive — archive.fo/FMgM3
>From a Sunday high of nearly $20,000 per digital coin, Bitcoin dropped more than 22% to a price as low as $15,262 on Thursday afternoon. Some see the drop as fallout from long-unresolved problems with Bitcoin’s infrastructure, and the increasingly intense civil war it has produced in the cryptocurrency community.
>Some recent Bitcoin buyers have described trying to actually use bitcoin for purchases, only to run into the reality of the network’s absurdly high transaction fees. Those fees have risen steadily for years due to crowding on the network.
Says the article. My take? All these currency-manipulators these people thought they could ride the coattails of, have royally fucked them over and profited billions. It's like I used to say, the Jews are gonna pump it up, then cash out all at once, killing the currency and fucking everyone over, while profiting millions and billions. It goes on to say:
>The long-running fight over how to fix the issue hit the mainstream as never before yesterday, when cryptocurrency pioneer Roger Ver appeared on CNBC. Ver was promoting Bitcoin Cash, a fork of Bitcoin created to address the digital currency’s scaling problems. Ver warned viewers that bitcoin could see “a mass exodus of people rushing for the door.” At the same time, a CNBC Twitter account was accused of “shilling” thanks to tweets that appeared to support Bitcoin Cash.
>Almost simultaneously, the cryptocurrency exchange Coinbase announced that it had halted trading in Bitcoin Cash over concerns that the exchanges’ employees may have engaged in insider trading—another possible shock to investor confidence.
>The conflicts and imperfections of the cryptocurrency world are nothing new, and neither are huge price dips—Bitcoin has seen two similarly sharp drops in just the last two months. And long-term supporters are optimistic that fixes for the underlying crowding issue, particularly a new feature known as Lightning Network, are on the way.
Bitcoin and Eliptical Curve Cryptography discussion welcomed. The most important thing to note about Bitcoin is that we won't be directly affecting its success until we move on to ECC itself.

Explaining this all as simply as possible
I'm the person who has been working on making a really simple explanation of everything. I've been attempting to cover everything anyone who wildly stumbles upon this might not know (so for example how RSA works, what big O notation means, what a nested loop is, as well as obviously explaining the grid and the whole point of all of this). Here's most of what I've done so far. I haven't had a lot of free time so I thought the most useful use of my time would be working on that "map" that VQC suggested we make. Obviously anyone is welcome to either suggest that this is complete shit or make changes or point out anything incorrect or work on their own version or anything like that. This work isn't about the individuals. It's about the result we get by working together. That's why if we can all get on the same level in terms of understanding, things might get done more quickly.

RSA #9
RSA General
Crumbs to focus on
In the (e,1) solution, d[t] = na+x
and a[t] = na
Therefore, if you can find the t value of this element, you can factor all semiprimes.
>Which column has NO gaps? [0]
>What is the pattern in COLUMN ZERO?
>One Row to Rule them All.
>A column that contains ALL and is the KEY to ALL the patterns.
>What are the patterns in COLUMN ZERO?
>If c is a semiprime, how many times does its square (c^2) appear in column zero? [5]
Why are there gaps?
The reason for the gaps may be because the VQC does not include decimal numbers. That is, because cells with gaps are the cells where the midpoint of a and b would not be a whole number. Or, worded another way, the difference between a and b would be an odd number.
There is a repeating pattern of gaps as you move horizontally from (0, n) to the right.
The pattern of gaps repeats every 2n if n is even.
The pattern of gaps repeats every n if n is odd.
>If first appearance of factor p is element t, second appearance will be at (p+1-t)
>p will be a factor of a in elements: t+p, t+2p, t+3p,…
as well as in elements:
>p+1-t, 2p+1-t, 3p+1-t,…
take d from all values of d[t] at (e,1) and there is a known pattern of (n-1) as factor in these values of d[t]-d that is different (increasingly) from the pattern of factors of n in a[t]
Why do the values in row one determine all the values in the columns below them?
Let me break that down.
Find every value of d - d[t]
There is a pattern of (n-1) being a factor.
Find every value of a[t].
There is a pattern of n being a factor.
The pattern in the first group of values is "increasingly different" from the second. We must catalogue these patterns.

RSA #8
Virtual Quantum Computer
Definition
The virtual quantum computer (VQC) is a grid made of infinite yet constructable sets that follow a known pattern. Like a quantum spreadsheet.
The grid is the superposition. The collapse of that superposition will be two input parameters, d and e which can be calculated easily for all integers, c, where c is the difference of two squares. Its purpose and our goal is to be able to factorize large semiprimes, all the way into the hundreds of digits, which would break the RSA cryptosystem.
When the integers that are the difference of two squares are arranged into the grid and their corresponding properties are shown, a pattern emerges that shows calculation instead of searching is possible.
Variables
The map's legend is {e:n:d:x:a:b}, where d is the result of removing the largest square from c AKA the square root,
e is the remainder,
n is what you add to d to be exactly halfway between a and b,
and x is what you add to a to make d.
c is any number that is the difference of two squares, so odd numbers are included. It is the number you want to factor.
f is what you add to c to make a square.
t is the third coordinate in the VQC..
Rules
Each cell of the grid (e,n) has infinite elements or ZERO elements.
Each cell with one value has infinite elements, since every element can make a new one.
By induction, a cell only needs one value to make infinite values, that's part of the power of this and is why it is a virtual quantum computer as a whole.
The t variable is what will allow you to walk across these infinite elements.
If a grid cell has elements, all elements are constructable from a finite set of root elements.
The grid is indexed using e, n, and t, where e is the rows, n is the columns, and t is the specific element in the cell-group.
Thus, only three variables are required to identify an element: e, n and t.
All products of odd numbers and all products of pairs of even numbers are the difference of two squares.
The x-intercept of the line that goes through the point containing the factors of c is (a + 1).
(1, 1) - the key
The values of a and b at 1,1 are related to the length of the longest side in right angled triangles.
The values here can be used to create the entire grid.
The values here determine the values of the rows to the left and right, which determine the values of the whole column.
Columns
Each cell at n=1 contains the roots of products in the column.
If c is a prime number, it will appear in one column exactly once.
If c is the product of two prime numbers that do not equal eachother, c will appear in two cells of one column.
All products (integers) c that are the sum of two squares appear (only) in columns where e=0,1,4,9,16,25…
All factors in a column are factors of the elements of the first cell in their column.
All Fermat primes (except) 3 appear in column one.
(e, 1)
(e, 1) = the genesis cell.
If a number at position t has a factor s, then s is a factor at (t+s), (t+2s) and so on for a at (e,1).
Also, if a number at position t has a factor s at (e+1), then s is a factor at (s+1-t), (2s+1-t), etc for a at (e,1).
n*a and n*b for any c can be found n places apart in the cell at (e,1).
(1, n)
The cells in row one where n=1 have a relationship with the cells 2n to the right and 2n to the left.
Each "a" from the first row equals na because xx+e = 2na and na is half of that. That's BIG part of the KEY
Each element in a cell can be generated by moving up (t-1 = x-2) or down (t+1 = x+2). Other variables can be generated from x.
Useful Equations and Notation
ab = c
dd + e = c
(d + n)(d + n)-(x + n)(x + n) = c
a + 2x + 2n = b
a = d - x
d = a + x
d = floor_sqrt(c)
e = c - (dd)
b = c / a
n = the difference between the square root d and the larger of the two squares
n = ((a + b) / 2) - d
d + n = number that is exactly halfway between a and b
d + n = i
x = d - a
x = (floor_sqrt(( (d+n)*(d+n) - c))) - n
x + n = j
f = e - 2d + 1
t = the variable that lets you traverse the infinite elements in for a given (e, n) that has values.
if (e is even) t = (x + 2) / 2
if (e is odd) t = (x + 1) / 2
Dnimeerf's Perpetual Muffin Oven
Howdy Pathgawds!
Along my musics, I found a someone who's working on a very similar thing from a different approach, but it's all related and nothing is coincidence.
That being said, he's a bit of a newfag, so to spare everyone his getting his own report thread, I'm just setting this up so that the RSA stays RSA and y'all can look into this if it piques your interest.
Dnimeerf, the floor is yours.

RSA #7
Our task is simple. We are going to completely break the entire RSA cryptosystem! We're bigshots now.
But wait, how are we going to just crack RSA? With the Virtual Quantum Computer! Quick rundown to follow.
The main mathematical task that must be achieved to break RSA is to be able to factorize any integer instantly. The VQC is a promising way to do that.
What is the VQC?
The virtual quantum computer (VQC) is a grid made of infinite yet constructable sets that follow a known pattern. Like a quantum spreadsheet.
The grid is the superposition. The collapse of that superposition will be two input parameters, d and e which can be calculated easily for all integers, c, where c is the difference of two squares.
So, when the integers that are the difference of two squares are arranged into the grid and their corresponding properties are shown, a pattern emerges that shows calculation instead of searching is possible.
Legend
The map's legend is {e:n:d:x:a:b}, where d is the result of removing the largest square from c AKA the square root,
e is the remainder,
n is what you add to d to be exactly halfway between a and b,
and x is what you add to a to make d.
c is any number that is the difference of two squares, so odd numbers are included.
n*a and n*b for any c can be found n places apart in the cell at (e,1).
Rules of the grid: global rules
Each cell of the grid (e,n) has infinite elements or ZERO elements.
Each cell with one value has infinite elements, since every element can make a new one.
By induction, a cell only needs one value to make infinite values, that's part of the power of this and is why it is a virtual quantum computer as a whole.
The t variable is what will allow you to walk across these infinite elements.
If a grid cell has elements, all elements are constructable from a finite set of root elements.
The grid is indexed using e, n, and t, where e is the rows, n is the columns, and t is the specific element in the cell-group.
Thus, only three variables are required to identify an element: e, n and t.
All products of odd numbers and all products of pairs of even numbers are the difference of two squares.
The x-intercept of the line that goes through the point containing the factors of c is (a + 1).
(1, 1) - the key
The values of a and b at 1,1 are related to the length of the longest side in right angled triangles.
The values here can be used to create the entire grid.
The values here determine the values of the rows to the left and right, which determine the values of the whole column.
(f, 1) is an interesting cell.
Columns
Each cell at n=1 contains the roots of products in the column.
If c is a prime number, it will appear in one column exactly once.
If c is the product of two prime numbers that do not equal eachother, c will appear in two cells of one column.
All products (integers) c that are the sum of two squares appear (only) in columns where e=0,1,4,9,16,25…
All factors in a column are factors of the elements of the first cell in their column.
All Fermat primes (except) 3 appear in column one.
(e, 1)
If a number at position t has a factor s, then s is a factor at (t+s), (t+2s) and so on for a at (e,1).
Also, if a number at position t has a factor s at (e+1), then s is a factor at (s+1-t), (2s+1-t), etc for a at (e,1).
Rows
(1, n)
The cells in row one where n=1 have a relationship with the cells 2n to the right and 2n to the left.
Each "a" from the first row equals na because xx+e = 2na and na is half of that. That's BIG part of the KEY
Each element in a cell can be generated by moving up (t-1 = x-2) or down (t+1 = x+2). Other variables can be generated from x.
Every single factor of any value of a in the first row will be referred to as s.
Useful Equations and Notation
ab = c
dd + e = c
(d + n)(d + n)-(x + n)(x + n) = c
a + 2x + 2n = b
a = d - x
d = a + x
d = floor_sqrt(c)
e = c - (dd)
b = c / a
n = the difference between the square root d and the larger of the two squares
n = ((a + b) / 2) - d
d + n = number that is exactly halfway between a and b
d + n = i
x = d - a
x = (floor_sqrt(( (d+n)*(d+n) - c))) - n
x + n = j
f = e - 2d + 1
t = the variable that lets you traverse the infinite elements in for a given (e, n) that has values.
if (e is even) t = (x + 2) / 2
if (e is odd) t = (x + 1) / 2

RSA #6
Our task is simple. We are going to completely break the entire RSA cryptosystem!
And how are we going to do that?! With the VQC! Quick rundown to follow.
The main mathematical task that must be achieved to break RSA is to be able to factorize any integer instantly. The VQC is a promising way to do that.
What is the VQC?
The virtual quantum computer (VQC) is a grid made of infinite yet constructable sets that follow a known pattern. Like a quantum spreadsheet.
The grid is the superposition. The collapse of that superposition will be two input parameters, d and e which can be calculated easily for all integers, c, where c is the difference of two squares.
When the integers that are the difference of two squares are arranged into the grid and their corresponding properties are shown, a pattern emerges that shows calculation instead of searching is possible.
Legend
The map's legend is {e:n:d:x:a:b}, where d is the result of removing the largest square from c AKA the square root,
e is the remainder,
n is what you add to d to be exactly halfway between a and b,
and x is what you add to a to make d.
c is any number that is the difference of two squares, so odd numbers are included.
n*a and n*b for any c can be found n places apart in the cell at (e,1).
Rules of the grid: global rules
Each cell of the grid (e,n) has infinite elements or ZERO elements.
Each cell with one value has infinite elements, since every element can make a new one.
By induction, a cell only needs one value to make infinite values, that's part of the power of this and is why it is a virtual quantum computer as a whole.
The t variable is what will allow you to walk across these infinite elements.
If a grid cell has elements, all elements are constructable from a finite set of root elements.
The grid is indexed using e, n, and t, where e is the rows, n is the columns, and t is the specific element in the cell-group.
Thus, only three variables are required to identify an element: e, n and t.
All products of odd numbers and all products of pairs of even numbers are the difference of two squares.
The x-intercept of the line that goes through the point containing the factors of c is (a + 1).
(1, 1) - the key
The values of a and b at 1,1 are related to the length of the longest side in right angled triangles.
The values here can be used to create the entire grid.
The values here determine the values of the rows to the left and right, which determine the values of the whole column.
Columns
Each cell at n=1 contains the roots of products in the column.
If c is a prime number, it will appear in one column exactly once.
If c is the product of two prime numbers that do not equal eachother, c will appear in two cells of one column.
All products (integers) c that are the sum of two squares appear (only) in columns where e=0,1,4,9,16,25…
All factors in a column are factors of the elements of the first cell in their column.
All Fermat primes (except) 3 appear in column one.
(e, 1)
If a number at position t has a factor s, then s is a factor at (t+s), (t+2s) and so on for a at (e,1).
Also, if a number at position t has a factor s at (e+1), then s is a factor at (s+1-t), (2s+1-t), etc for a at (e,1).
Rows
(1, n)
The cells in row one where n=1 have a relationship with the cells 2n to the right and 2n to the left.
Each "a" from the first row equals na because xx+e = 2na and na is half of that. That's BIG part of the KEY
Each element in a cell can be generated by moving up (t-1 = x-2) or down (t+1 = x+2). Other variables can be generated from x.
Every single factor of any value of a in the first row will be referred to as s.
Want an even better quick rundown? Read VQC's introduction.
Useful Equations and Notation
ab = c
dd + e = c
(d + n)(d + n)-(x + n)(x + n) = c
a + 2x + 2n = b
a = d - x
d = a + x
d = floor_sqrt(c)
e = c - (dd)
b = c / a
n = the difference between the square root d and the larger of the two squares
n = ((a + b) / 2) - d
d + n = number that is exactly halfway between a and b
d + n = i
x = d - a
x = (floor_sqrt(( (d+n)*(d+n) - c))) - n
x + n = j
f = e - 2d + 1
t = the variable that lets you traverse the infinite elements in for a given (e, n) that has values.
if (e is even) t = (x + 2) / 2
if (e is odd) t = (x + 1) / 2